Much of Origami is algorithmic (algorithm = procedural solution to a problem). A rabbit ear is an algorithm, one knows how to fold it on a corner – double rabbit ear is the same solution, folded two simultaneously. Petal fold is also a standard maneuver which got me thinking of the Sato Rose algorithm.
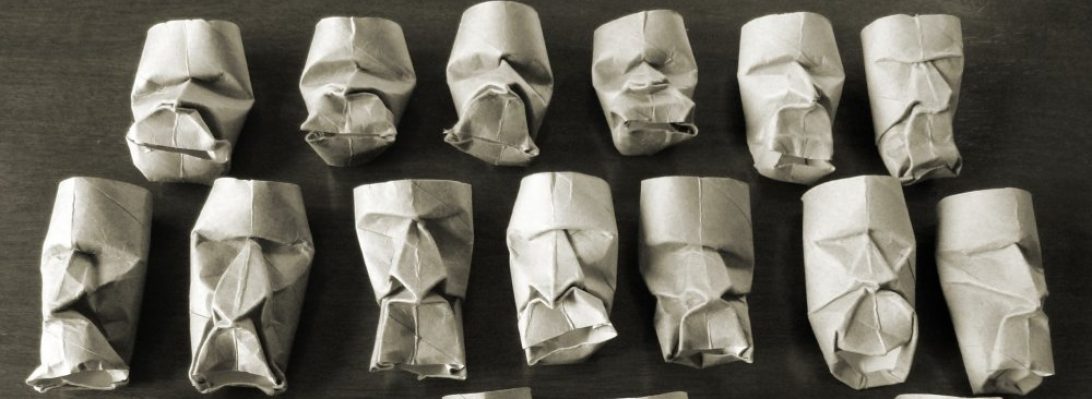
I like this algorithm particularly because of the free-form nature of much of the folding, and the way it seems to “fit” a pentagon. I decided to use the same folding algorithm but try it with other regular polygons – I tried triangle(3), square(4), pentagon(5), hexagon(6), heptagon(7), octagon(8), nonagon(9) but gave up on the decagon(10).
The algorithm involves “nearly” bisecting each vertex to form an echo shape at the centre of the sheet – you then halve that internal echo to create a slightly offset echo and use that as the basis of a “kawasaki twist”
Once the twist has happened, you begin dividing the protruding flaps into petals.
The Sato (a modified Kawasaki II rose variation) generates 3 layers of petals arranged in a lovely spiral from a tight central petal cluster. 
All shapes are NOT created equal for this algorithm – although you CAN use other polygons, each one has different effects on the resultant bloom shape.
The LOWER the number of vertices, the LARGER the outer 2 petal layers are (these are the ones that receive most modelling treatment and hence can effect the overall “rosy-ness” of the flower) and the FLATTER and TIGHTER the inner bud is. You can see that the TRIANGLE has huge outer petals.
As the number of vertices increases the flower centre protrudes and is MUCH more difficult to make tight and compact so gapes, the outer petals shrink and the bloom becomes (to my eye at least) less beautiful.
I think there is a reason the PENTAGON works best, and am sure there is mathematics to back up my gut feeling (although that maths is beyond me at the moment). The Pentagon, to me, provides the ideal ratio of outer petal size to inner bud, but this has been an interesting investigation as I am sure I was not aware of the dynamics of the fold nor the effects the parameters (in this case the number of vertices) had on the result.